Les fondamentaux – Chapitre 2 – Caractéristiques d’une image médicale
E. Durand et E. Blondiaux
Plan du chapitre
- Numérisation, pixels, voxels
- Résolution spatiale
- Bruit
- Contraste
- Images en projection et images en coupes
- Présentation et orientation des images
- Archivage
Une image correspond à la mesure localisée d’un signal physique d’un objet1 dans l’espace, généralement en deux dimensions (2D) ou en trois dimensions (3D). On explore ainsi une partie de l’espace appelée « champ de vue » ou field of view (FOV). Ce champ de vue peut concerner l’organisme entier (imagerie « corps entier ») ou bien être ciblé sur une partie de l’organisme.
1. Le terme d’« objet » est ici utilisé comme en optique où l’on observe l’image d’un objet. En imagerie médicale, l’objet observé est le corps humain ou une partie du corps.
Numérisation, pixels, voxels
Cette image est désormais numérique ou numérisée pour presque toutes les techniques d’imagerie médicale (les films radiologiques à base de sels d’argent, autrefois utilisés, ont désormais disparu ; de même que la photographie numérique a remplacé les anciens films photographiques). On range donc dans des cases d’une mémoire d’ordinateur les mesures des signaux physiques. Comme le nombre de cases est en quantité finie, on ne peut plus conserver une mesure continue de l’information, c’est-à-dire connaître la valeur du signal en chaque point de l’espace ; on est obligé de découper l’objet matériel en petits éléments réguliers appelés voxels (volume elements). Les signaux mesurés dans les voxels sont rangés dans de petits rectangles de l’image en 2D (en petits parallélépipèdes en 3D) qui sont appelés pixels (picture elements). La notion de voxel se rapporte donc à l’élément matériel tandis que la notion de pixel se rapporte à l’image (figure 2.1).
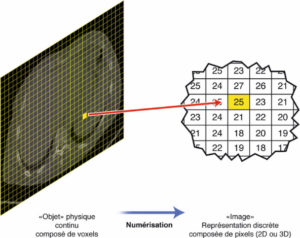
Numérisation d’un objet en image.
Dessin : Emmanuel Durand.
Le signal est donc uniforme au sein d’un pixel dans l’image, alors qu’il ne l’est pas au sein d’un voxel dans l’objet exploré. Ce passage d’un objet réel continu à une image composée de pixels – donc discrète –, appelée conversion analogique-numérique, peut être la source d’artefacts. En particulier, si la taille des pixels est trop grosse, on risque de perdre une partie des détails. Le nombre de pixels dans chacune des dimensions s’appelle la matrice. Par exemple, un champ de vue de 12,8 cm découpé en pixels de 1 mm de côté aura une matrice de 128. Plus la matrice est grande, plus la taille des pixels est petite et plus il est donc théoriquement possible de voir des détails fins (figure 2.2). La matrice est souvent composée de puissances entières de 2, pour des raisons liées aux calculs en traitement de l’image. De même, le nombre de pixels dans les deux dimensions est souvent le même.
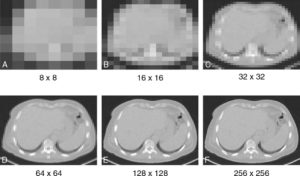
Effet de la matrice (une petite matrice correspond à de gros pixels).
Dessin : Emmanuel Durand.
Résolution spatiale
La résolution spatiale est la capacité à distinguer des structures fines dans l’image. Au sens strict, la résolution spatiale est le nombre de paires de lignes qu’on peut distinguer dans une image par unité de longueur. Par exemple, si on distingue deux points séparés de 2 mm, mais qu’on ne distingue plus des points plus rapprochés, on dira que la résolution spatiale est de 0,5 mm–1. Par abus de langage, on parle le plus souvent d’une résolution de 2 mm dans ce cas.
La résolution est bien sûr conditionnée par la taille des pixels. Par exemple, si la taille d’un pixel est de 2 mm, la résolution la plus fine qu’on puisse espérer voir est de 0,25 mm− 1, c’est-à-dire des structures espacées de 4 mm (figure 2.3).
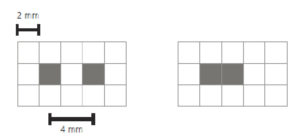
On ne peut distinguer deux pixels noirs que s’ils sont espacés d’un pixel blanc (A) ; sur la figure de droite, on ne distingue qu’une seule structure (B). La résolution spatiale la plus fine permise est donc 1/(2 pixels).
Dessin : Emmanuel Durand.
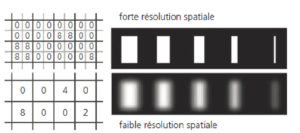
Toutefois, s’il n’est pas possible de voir une résolution plus fine que ce que permet la taille des pixels, cette dernière ne fait pas tout. En effet, la qualité de l’instrument d’imagerie a un rôle majeur et si la résolution intrinsèque de l’appareil est mauvaise, découper l’image en pixels très fins ne résoudra rien (figure 2.4).
La taille des pixels peut limiter la résolution spatiale, mais la résolution spatiale n’est pas la taille des pixels : elle dépend aussi de la qualité de l’appareil d’imagerie !

La taille des pixels est la même dans les deux figures (A, B) ; pourtant, la figure de gauche a une bien meilleure résolution (A).
Dessin : Emmanuel Durand.
Lorsque des structures sont plus petites que ce que permet de voir la résolution spatiale, elles peuvent :
- ne pas être visibles ;
- être visibles mais floues (figure 2.4) ;
- être vues mais avec un niveau de signal incorrect, par moyennage avec les structures qui les entourent ; on parle alors d’effet de volume partiel (figure 2.5).
Effet de volume partiel.
En haut, la résolution spatiale est suffisante pour mesurer le signal avec une intensité correcte ; en bas, une résolution spatiale trop faible entraîne en moyennage des structures les plus petites avec leur entourage (ici, les structures sont sur un fond à signal nul : le niveau de signal est donc sous-estimé) : il s’agit d’un effet de volume partiel.
Dessin : Emmanuel Durand.
Bruit
Dans le domaine du traitement du signal et de l’image, le bruit correspond à un phénomène aléatoire qui se surajoute à l’image idéale. Probablement la meilleure approche pour comprendre le bruit est de comprendre que si l’on acquiert plusieurs fois l’image d’un même objet, immobile et inchangé, on n’observera pas exactement le même résultat : la différence est liée au bruit. De la même manière, en lançant plusieurs fois un dé, on n’obtient pas le même résultat : c’est aléatoire (figure 2.6).
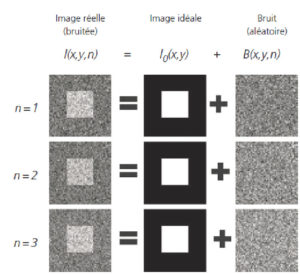
Si l’on répète l’acquisition d’une image à différents temps (n = 1, n = 2, etc.), on obtient des images différentes d’une fois à l’autre.
Dessin : Emmanuel Durand.
La partie constante est l’image idéale, la partie variable est le bruit.
Comme tout phénomène aléatoire, le bruit est caractérisé par son écart type (racine carrée de la variance), qu’on note σ.
Pour quantifier le niveau de bruit, on compare généralement l’intensité du signal avec l’écart-type du bruit pour déterminer le rapport signal sur bruit (RSB) :
où S est l’intensité du signal. Le bruit dans l’image peut gêner l’interprétation et, à l’extrême, rendre les images complètement illisibles. La présence de bruit va également détériorer la résolution spatiale puisqu’il peut être impossible de distinguer des structures trop petites dans une image très bruitée (figure 2.7).

Différents niveaux de rapports signal sur bruit (RSB).
Un RSB de 1 permet encore de distinguer les plus grosses structures mais plus les structures les plus fines.
Dessin : Emmanuel Durand.
Contraste
Un diagnostic est généralement fait en discernant le signal anormal d’une lésion au sein d’un organe normal. C’est donc le contraste entre les deux qui permet le diagnostic. Le signal de l’organe normal est parfois appelé « bruit de fond » en français. Ce terme n’est pas très heureux car il fait référence au bruit (aléatoire) alors qu’il ne s’agit pas de bruit ici. Le terme anglais background est plus adapté.
Si l’on note S1 le signal de la lésion et S2 le signal de fond, le contraste est traditionnellement défini comme : C = | S1 – S2 | / | S1 + S2 |
Un signal de 6 sur un fond de 2 donne donc un contraste de 0,5. Toutefois, sur une image numérique, il est aisé de changer le contraste à volonté. Dans l’exemple précédent, si l’on soustrait la valeur 4 à l’image, les deux valeurs précédentes deviennent respectivement + 2 et − 2 avec un contraste qui devient infini. Plus intéressant est donc de considérer le rapport contraste sur bruit (RCB) : RCB = C = | S1 – S2 | / σ
Images en projection et images en coupes
L’objet étudié est fondamentalement tridimensionnel. Certaines modalités d’imagerie fournissent une image tridimensionnelle (imagerie en coupes) ; d’autres ne permettent d’obtenir qu’une image 2D (tableau 2.1). Il s’agit donc d’une projection de l’objet initial, comme une ombre chinoise (figure 2.8). On perd alors l’information de profondeur, la quantification devient difficile et les superpositions peuvent gêner l’interprétation.
Tableau 2.1
Types et mécanismes des différentes modalités d’imagerie
|
Type |
Mécanisme |
Modalité |
2D/3D |
|
Morphologique |
Absorption des rayons X |
Radiographie Angiographie numérisée |
Projection 2D |
|
Angiographie rotationnelle TDM (scanner) |
3D |
||
|
Réflexion des ultrasons |
Échographie |
Coupes 2D |
|
|
Échographie 3D |
3D |
||
|
Mixte |
Échos de l’aimantation des noyaux |
IRM |
3D |
|
Fonctionnelle |
Émission de photons gamma |
Scintigraphie |
Projection 2D |
|
Tomoscintigraphie
|
3D |
||
|
Émission de positons |
TEP |
3D |
Présentation et orientation des images
Par convention, les images sont présentées de la même façon au sein d’une modalité, qu’elle soit en projection ou en coupes (figure 2.8) :
• en projection de face ou en coupe coronale (ou frontale), la droite du patient est présentée à gauche de l’écran : comme si on regardait simplement le patient de face ;
• sur une vue axiale (ou transverse), la droite du patient est toujours située à gauche de l’écran : comme si on regardait le patient – allongé sur le dos – depuis ses pieds ;
• sur une vue sagittale ou de profil, l’image est présentée avec la partie antérieure du patient à gauche de l’écran, comme si on regardait le patient de profil gauche (à l’exception des images d’échographie sur lesquelles le pôle crânial du patient est présenté à gauche de l’écran)
• les images de scintigraphie planaire (projections) sont toujours représentées comme si l’observateur avait le point de vue de la caméra (voir chapitre 5).
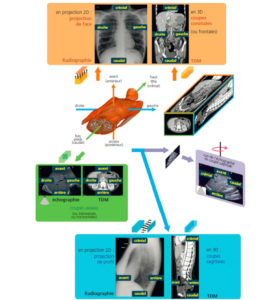
Orientation conventionnelle des images : coupes axiales, coronales et sagittales de TDM ; projections de face et profil en radiographie.
L’orientation est normalisée pour ces différentes images. Elle est la même en IRM et en tomoscintigraphie. Les coupes sagittales d’échographie sont représentées différemment, le pôle crânial étant placé à gauche de l’écran.
Dessin : Emmanuel Durand.
Archivage
Les images médicales sont enregistrées sous un format de stockage et d’échange appelé digital imaging communication in medicine (DICOM) qui contient, outre l’image elle-même, des métadonnées la caractérisant (identité du patient, date et heure d’acquisition, type d’appareil, paramètres d’acquisition détaillés, etc.). Dans les établissements de santé, les images sont désormais archivées dans un système en réseau appelé Picture Archiving and Communication System (PACS), habituellement consultable également par les correspondants.
 |
Chapitre suivant |
 |
Retour au sommaire |
