Les fondamentaux – Chapitre 9 – Reconstruction tomographique
F. Ben-Bouallègue , E. Durand et D. Mariano-Goulart
Plan du chapitre
- Introduction
- Notion de projection
- En tomoscintigraphie
- En tomodensitométrie
- Problème direct – problème inverse
- Résolution du problème inverse en résolvant le système d’équations
- Rétroprojection
Objectifs
L’imagerie médicale repose schématiquement sur l’acquisition d’un signal physique, sur l’optimisation de ce signal (filtrages), sur sa mise en forme pour en faciliter l’utilisation médicale (reconstructions), puis sur son analyse (extraction d’éléments diagnostiques) qui fera l’objet du chapitre 10. Parmi les divers types de reconstructions possibles, la reconstruction tomographique joue un rôle central en tomodensitométrie (TDM), en imagerie par résonance magnétique (IRM) et en tomoscintigraphie d’émission. Elle fait l’objet de ce chapitre qui explique en quoi la reconstruction d’images tomographiques relève d’un problème linéaire mal conditionné et sur quels principes fonctionnent les algorithmes de rétroprojection filtrée et les techniques itératives de reconstruction. Il exclut tout formalisme mathématique, mais pourra servir d’introduction à l’approfondissement plus complet [1], mais aussi plus scientifique de la tomographie médicale.
Introduction
Avec W. Röntgen et H. Becquerel, puis la famille Curie, le XIXe siècle finissant avait vu éclore une physique des rayonnements ionisants qui permettait pour la première fois de visualiser les organes internes d’un patient de façon non invasive. Le développement de l’imagerie radiologique qui suivit très vite, puis de l’imagerie scintigraphique resta cependant longtemps cantonné à la production d’images de projections où les signaux issus des divers plans perpendiculaires au rayonnement incident se superposaient sur un plan unique, rendant complexe l’interprétation médicale. Les solutions théoriques qui permirent de résoudre cette difficulté et de disposer d’une imagerie volumique ou reconstruite en coupes existaient pourtant dès le début du XXe siècle, avec les travaux des mathématiciens J. Radon en 1917 et S. Kaczmarz en 1937.
Mais il fallut attendre l’intervention d’un ingénieur talentueux, G.N. Hounsfield, au tout début des années 1970, le développement des calculateurs numériques qui accompagna la conquête de la Lune, puis le parrainage financier d’une société d’édition musicale qui bénéficiait dans les années 1960 du succès phénoménal de quatre chanteurs à la mode venus de Liverpool pour que naisse la tomographie médicale et que les premiers scanners prennent peu à peu la place qu’on leur connaît de nos jours dans le diagnostic médical.
Notion de projection
D’une manière assez générale, on cherche à obtenir des images en trois dimensions (3D) mais les acquisitions se font généralement en deux dimensions (2D). C’est le cas aussi pour la vision : nous percevons sur notre rétine (2D) l’image 2D d’un monde en 3D ; on parle de projection (figure 9.1A). Cela s’applique aussi à la plupart des techniques d’imagerie médicale : TDM, tomoscintigraphie, TEP et, dans certains cas, à l’IRM3.
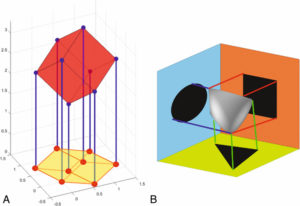
Projection.
A. Une figure 3D est projetée sur un plan et transformée en figure 2D, comme une ombre projetée. B. Projeter selon différentes directions conduit à différentes projections à partir d’un même objet.
Dessin : Emmanuel Durand.
Le fait de projeter entraîne une perte d’information : à partir de l’ombre d’un objet, on ne peut pas déterminer l’objet lui-même. En revanche, la combinaison de différentes projections permet d’avoir une meilleure idée de l’objet de départ (figure 9.1B). C’est le principe général de la reconstruction tomographique, objet de ce chapitre.
Du point de vue informatique, on considère qu’une image est composée d’une matrice de voxels, considérés comme homogènes et caractérisés chacun par la valeur du signal physique qu’il contient. En pratique, la projection selon un axe vertical ou horizontal consiste simplement à faire la somme de toutes les valeurs le long d’une ligne ou d’une colonne (figure 9.2A). Bien entendu, une projection selon une direction oblique est plus complexe, mais le principe est le même. Projeter une image 3D sur un plan 2D est difficile à représenter et plus complexe à écrire en équations. Dans tout ce qui suit, nous partirons donc d’une image en 2D pour la projeter sur une ligne en 1D, ce qui est plus simple à la fois à représenter et à modéliser en équations. Le principe reste strictement le même pour passer du 3D au 2D.
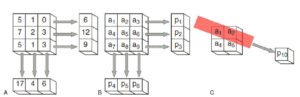
A. Projection d’une matrice de voxels en lignes ou en colonnes. B. Si l’on représente les nombres de la matrice de manière symbolique par ai,j, on peut facilement calculer les valeurs des projections, par exemple : p1 = a1 + a2 + a3 ou p4 = a1 + a4 + a7. C. Le calcul des projections obliques est plus compliqué, faisant appel à des sinus et cosinus, mais se fait sur le même principe, par exemple ici p10 ≈ 0,8 × a1 + 0,9 × a2 + 0,15 × a5.
Dessin : Emmanuel Durand.
En tomoscintigraphie
En tomoscintigraphie, lorsqu’on utilise un collimateur parallèle, le signal de chaque voxel correspond au nombre de photons gamma résultant de l’activité dans ce voxel, lui-même proportionnel à la concentration de radioactivité. Le nombre total de photons détectés sur un élément de détection de la gamma-caméra correspond exactement à la somme des signaux des voxels le long d’une perpendiculaire au détecteur4 (figure 9.3 et voir figure 9.2B). L’image captée par le détecteur (2D) est donc bien une projection de l’activité de l’ensemble des voxels (3D). Il en va de même en TEP avec la détection en coïncidence.
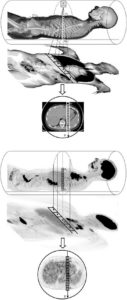
Projections et reconstructions en tomodensitométrie et en tomoscintigraphie.
Dessin : Denis Mariano-Goulart.
D’une manière générale, on peut exprimer la valeur de chaque projection comme :
pk = sum from {i} rk,i × ai (1)
où ai désigne le signal du voxel i, pk la projection k et les coefficients rk,i la proportion de volume du pixel i qui se projette effectivement dans la projection k. Dans l’exemple de la figure 9.2B, on aurait par exemple r1,1 = 1 ; r1,4 = 0 et r2,4 = 1. En faisant tourner la gamma-caméra autour du patient, on peut ainsi obtenir de très nombreuses projections sous des angles différents. En TEP, la détection en coïncidence permet d’obtenir simultanément des projections dans toutes les directions visibles du détecteur.
En tomodensitométrie
En TDM, on envoie un faisceau de rayons X d’intensité I0 ; après avoir traversé le patient, ce faisceau ressort de manière atténuée avec une intensité Ii. La loi générale d’atténuation est :
Ii = I0 × e-μL (2)
après la traversée d’une longueur L d’un milieu de coefficient d’atténuation μ (voir figure 9.3).
Si l’on considère la traversée des 3 voxels numérotés 1, 2 et 3 comme sur la figure 9.2B, en désignant par d la largeur du voxel, l’atténuation de la première ligne de projection sera donnée par :
I1 = I0 × e-µ1d × e-µ2d × e-µ3d = I0 × e-( µ1 + µ2 + µ3)d (3)
L’opération n’est donc pas une simple somme, comme dans la tomoscintigraphie. Cependant, en transformant l’équation 3, on aboutit facilement à :
ln(I0 /I1) / d = µ1 + µ2 + µ3 (4)
On est donc ramené exactement au problème précédent de la tomoscintigraphie où chaque projection est la somme des signaux des voxels. Dans le cas de la TDM, le signal d’un voxel correspond au coefficient d’atténuation. Comme en tomoscintigraphie, on fait tourner le tube et le détecteur autour du patient pour acquérir de très nombreuses projections sous différents angles.
Problème direct – problème inverse
L’acquisition de l’image consiste à mesurer l’ensemble des projections pk. La reconstruction de l’image consiste à en déduire l’ensemble des signaux des voxels ai qui sont des inconnues. Modéliser l’acquisition revient à déterminer l’ensemble des coefficients rk,i qui déterminent les projections. En gros, cela revient à être capable de modéliser l’acquisition des projections, c’est-à-dire, connaissant les valeurs des voxels ai, à être capable de prédire les projections pk. On appelle cela le problème direct. C’est finalement assez simple si l’on connaît la géométrie de l’acquisition.
Dans la « vie réelle », on ne connaît pas les valeurs des voxels ; c’est même justement ce qu’on cherche à déterminer à partir des projections qu’on a pu mesurer. On appelle cela un problème inverse. On dispose donc de données connues, les projections pk, d’un système d’équations linéaires du style de l’équation 1 : pk = sum ( rk,i × ai). Il suffit donc en théorie de trouver les inconnues ai en résolvant ce système.
Résolution du problème inverse en résolvant le système d’équations
Dans le cas simplifié représenté par la figure 9.4, on a un système de 4 équations à 4 inconnues (a,b,c et d).
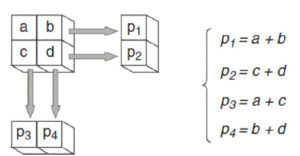
Cas simplifié.
Dessin : Emmanuel Durand.
Il est donc en théorie relativement facile de le résoudre, en particulier si l’on dispose de calculateurs électroniques. En pratique, si l’on considère une image 3D en matrice 256 × 256 × 256, on a donc 16 777 216 inconnues ; il faut un nombre d’équations au moins égal pour pouvoir le résoudre. Cette résolution mathématique théorique nécessite alors beaucoup de calculs élémentaires et est mise en défaut par une propriété propre à la plupart des grands systèmes d’équations linéaires.
Pour l’illustrer, simplifions encore notre exemple en nous attachant à reconstruire une image constituée de deux pixels (a,b) seulement, au moyens de deux projections p1 et p2.
Les deux équations de projection s’écrivent :
D1 : p1 = r11 · a + r12 · b
D2 : p2 = r11 · a + r12 · b
Dans un graphe où l’on place en abscisse les valeurs possibles de a et en ordonnée celles de b, ces deux équations sont celles de deux droites D1 et D2 dont l’intersection est la solution (a,b) du système, donc la coupe recherchée. Si ces deux équations sont très différentes l’une de l’autre (figure 9.5A), une petite erreur sur la modélisation des coefficients rij ou sur la mesure des projections pi par l’appareil d’imagerie conduit à une erreur minime (a′,b′) sur l’estimation de l’intersection de ces deux droites, donc de l’image recherchée. En revanche, si les deux équations ont des coefficients proches, la moindre erreur sur le modèle (rij) ou sur les mesures de projections (pi) donnera un résultat complètement erroné pour la coupe, avec une solution (a′,b′) très éloignée de la vérité (figure 9.5B). En tomographie, où l’on acquiert beaucoup de projections très proches les unes des autres, cette seconde situation est malheureusement la règle.
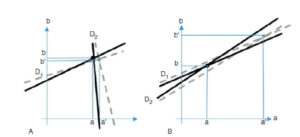
A, B. Les droites grises en pointillées représentent des projections légèrement différentes des projections exactes, en traits pleins noirs.
On constate que si deux projections sont proches, une erreur importante sur l’estimation de l’image en coupe (a, b) peut subvenir si ces projections sont faiblement bruitées.
Dessin : Denis Mariano-Goulart.
Pour cette raison, la technique qui semble a priori la plus simple, résoudre un système d’équations par un algorithme standard (déterminant, pivot de Gauss, etc.), ne peut pas être utilisée. Cela va donc nécessiter l’utilisation d’algorithmes plus complexes que ceux classiquement utilisés en algèbre.
Rétroprojection
Pour comprendre comment se fait la reconstruction, nous avons besoin de décrire un nouvel opérateur appelé « rétroprojection ». Mathématiquement, la rétroprojection consiste à sommer, au sein d’un pixel image i, chacune des projections k auquel il participe, pondérées par le coefficient rk,i.
Projection : pk = sum from {i} rk,i × ai (5)
Rétroprojection : bi = sum from {k} <?> rk,i × pk (5)
Concrètement, il s’agit de « propager » la valeur projetée, dans la direction de la projection, sur tous les pixels concernés (figure 9.6), et de sommer le résultat pour toutes les projections. On voit ici que l’image de rétroprojection (normalisée) ne correspond pas vraiment à l’image de départ : la rétroprojection n’est donc pas l’opération inverse de la projection. Cependant, on constate des similitudes ; par exemple, le voxel central a la valeur la plus élevée sur les deux images ; l’angle supérieur gauche a la plus faible valeur dans les deux cas.
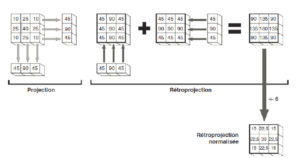
Principe de la rétroprojection.
On prend les projections verticales et on les rétroprojette verticalement en « propageant » chaque valeur sur toute la colonne ; on fait de même avec les projections horizontales, puis on ajoute l’ensemble des rétroprojections. On peut ensuite normaliser la rétroprojection en divisant par le nombre de rétroprojections (6 ici). N.B. : pour modéliser correctement une image de 3 × 3 = 9 pixels, il faudrait au moins 9 projections. On en a pris moins ici par souci de simplification.
Dessin : Emmanuel Durand.
L’application de cet opérateur de rétroprojection pour la reconstruction des images à partir de projections produit des images qui ressemblent à l’image originale, sans lui être identique (figure 9.7). Cela illustre encore le fait que la rétroprojection n’est pas l’opérateur inverse de la projection.
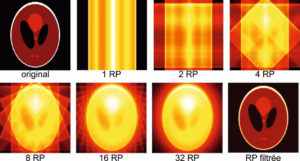
Rétroprojection.
À partir d’une image originale (simplifiée) dont on a déterminé les projections dans diverses directions, on construit les rétroprojections avec un nombre de projections allant de 1 à 32 ; on voit alors se dessiner progressivement une représentation imparfaite de l’image originale. Seule une opération de filtrage permettra de retrouver une représentation fidèle de l’image originale.
Dessin : Emmanuel Durand.
Rétroprojection filtrée
La simple opération de rétroprojection ne permet donc pas d’obtenir une image fidèle ; on voit en effet, sur les images reconstruites, des artefacts en étoile ou en halo correspondant aux traînées de rétroprojection (figure 9.8 et voir figure 9.7). On constate ainsi sur la figure 9.6 que le contraste entre le centre et les bords est plus faible sur l’image reconstruite par rétroprojection que sur l’image originale. Avant de rétroprojeter, il faut donc accentuer le contraste pour compenser cet effet. Ce filtrage, appelé « filtre rampe » et fondé sur des bases mathématiques solides, peut s’illustrer de la manière suivante : on va renforcer le contraste en changeant la valeur rétroprojetée ; au lieu de prendre la valeur obtenue par projection (voir figure 9.6), on prendra le double de cette valeur diminuée des deux tiers des valeurs des projections adjacentes.
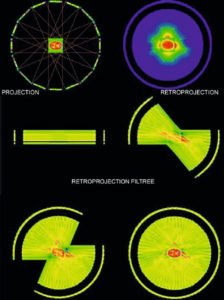
Illustration des opérations de projection, de rétroprojection et de rétroprojection filtrée dans le cas d’une tomoscintigraphie cérébrale.
Dessin : Denis Mariano-Goulart.
Lorsqu’on multiplie le nombre de rétroprojections filtrées, on obtient une image fidèle à l’objet original (figure 9.9).
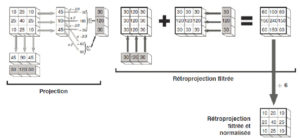
Rétroprojection filtrée.
Par rapport à la rétroprojection simple, au lieu d’utiliser la valeur de projection, on prend le double et on retranche les deux tiers de chaque projection voisine. Dans cet exemple simple, la reconstruction permet de trouver l’objet qu’on a projeté. En pratique, il faut généralement prendre davantage de projections pour obtenir une reconstruction correcte (ici, on n’a que 2 projections de 3 pixels, soit 6 valeurs numériques ; dans le cas général, il en faut davantage pour reconstruire une image de 3 × 3 = 9 pixels).
Dessin : Emmanuel Durand.
Reconstruction itérative
L’algorithme de rétroprojection filtrée ne nécessite pas de calculateurs électroniques puissants et a été universellement utilisé en TDM et en tomoscintigraphie jusqu’à la fin du XXe siècle. Dans les années 1970, exploitant des travaux initialement dus au mathématicien polonais S. Kaczmarz, une nouvelle famille d’algorithmes dits itératifs (ou algébriques) s’est peu à peu imposée en imagerie scintigraphique, puis en radiologie. Son développement, rendu possible par la puissance de calcul des ordinateurs modernes, a permis de réduire l’irradiation des patients en radiologie tout en se contentant, en particulier en TEP, de données de projections parfois incomplètes (ce que l’algorithme de rétroprojection filtrée ne permet pas). Ces techniques permettent en outre de mieux prendre en compte le mauvais conditionnement du problème tomographique (régularisation) et de mieux corriger certains artefacts inhérents aux acquisitions des projections (auto-atténuation en médecine nucléaire). Cette famille d’algorithmes a en commun de déterminer la coupe compatible avec les projections effectivement acquises en évaluant un écart entre celles-ci et des projections calculées à partir d’une estimation de la solution, puis en corrigeant l’estimation de la coupe au moyen de l’écart constaté.
En d’autres termes, on est capable d’acquérir des projections du corps humain en utilisant un appareil d’imagerie (TDM ou gamma-caméra). Comme nous l’avons vu, l’opération inverse n’est pas simple. En revanche, si l’on dispose d’une image informatique de l’objet, il est très simple d’en faire des projections au moyen d’un programme informatique. On peut alors comparer les projections de l’objet et les projections de son image. Le principe des techniques itératives est donc de trouver, par approximations successives, l’image qui donnera les mêmes projections que celles obtenues lors de l’acquisition (figure 9.10).
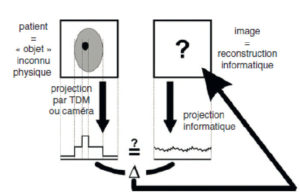
Principe des techniques itératives.
On ne peut pas simplement réaliser l’opération inverse de la projection, mais on peut projeter informatiquement l’image reconstruite, comme on peut projeter l’objet. La comparaison des projections permet de modifier l’image reconstruite pour la rendre plus proche de l’objet.
Dessin : Emmanuel Durand.
Le prototype de ce type d’algorithme itératif, ART (algebraic reconstruction technique), procède de la manière suivante : à partir d’une première coupe quelconque, l’algorithme ajuste étape par étape la coupe recherchée au moyen d’une rétroprojection normalisée par de l’écart entre les projections effectivement mesurées et celles déduites de la coupe en cours d’évaluation (figure 9.11).
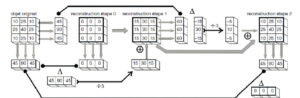
Reconstruction itérative : exemple simplifié.
On part d’une image vierge (composée de 0) et on la projette verticalement. On compare cette projection (0 ; 0 ; 0) à la projection de l’objet dans la même direction (45 ; 90 ; 45). On en fait la différence qu’on normalise en divisant par 3 (car somme sur 3 pixels). On obtient (15 ; 30 ; 15) qu’on va rétroprojeter dans la même direction verticale et l’ajoutant à l’image de départ. On obtient alors la reconstruction à l’étape 1. On va maintenant faire une projection de cette nouvelle image reconstruite dans une autre direction, ici horizontale ; on obtient (60 ; 60 ; 60) qu’on va comparer à la projection de l’objet dans la même direction (45 ; 90 ; 45). On normalise la différence en divisant par 3 pour obtenir (–5 ; 10 ; –5). On rétroprojette cette projection horizontalement et on l’ajoute à l’image précédemment reconstruite. Dans cet exemple simple, la reconstruction permet de trouver l’objet qu’on a projeté dès la deuxième itération. En pratique, il faut généralement prendre davantage de projections pour obtenir une reconstruction correcte.
Dessin : Emmanuel Durand.
L’algorithme itératif qui s’est imposé depuis les années 2000 opère itérativement comme ART, mais la correction est cette fois multiplicative et l’écart est évalué par le rapport entre projections acquises et estimées.
Plus précisément, cet algorithme fonctionne en multipliant chaque valeur inconnue de pixel i par la moyenne pondérée (par les coefficient ri,j) des rapports entre les projections j acquises et estimées qui concernent ce pixel i (voir figure 12). Il porte le nom de MLEM (pour maximum likelihood-expectation-maximisation), d’OSEM dans sa version accélérée ou de MAP-OSEM dans sa version régularisée.
6.6.Le lecteur pourra reprendre l’exemple de la figure 9.12 en initialisant la matrice à l’étape 0 avec autre chose que des 1. Il pourra alors constater qu’on aboutit à une convergence de l’algorithme sur une solution différente. Par exemple, une initialisation avec :
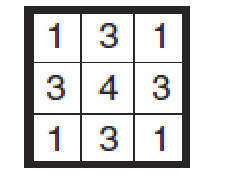
conduirait en une seule itération à la solution :
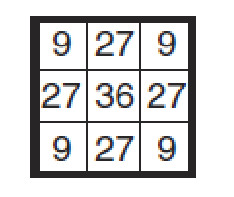
Cela illustre le fait qu’il peut y avoir plusieurs solutions au problème lorsque le nombre de projections est insuffisant.
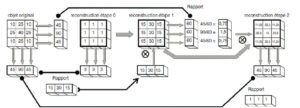
Algorithme itératif multiplicatif.
On part d’une image vierge composée de 1 qu’on projette dans une première direction (ici verticale) ; on compare la projection obtenue (3 ; 3 ; 3) avec la projection de l’objet dans la même direction (45 ; 90 ; 45). Le rapport (15 ; 30 ; 15) va être rétroprojeté dans la même direction (verticale) pour servir de facteur multiplicatif pour obtenir l’image reconstruite à l’étape 1. En partant de cette dernière image, on réalise une projection dans une autre direction et on continue sur le même principe. Dans cet exemple simple, la reconstruction permet d’atteindre une convergence dès la deuxième itération. Le résultat obtenu n’est pas tout à fait l’image de départ : en pratique, il faut généralement prendre davantage de projections pour obtenir une reconstruction correcte.
Dessin : Emmanuel Durand.
Essentiel à retenir
- Les images acquises en radiographie et en scintigraphie sont des images de projection.
- Reconstruire une image en coupe revient à résoudre un grand système mal conditionné d’équations linéaires.
- Les techniques de reconstruction incluent l’algorithme de rétroprojection filtrée (et autres techniques analytiques apparentées) et les techniques itératives (ou algébriques) parmi lesquelles MLEM et sa variante OSEM sont les plus utilisées.
- Les techniques itératives présentent divers avantages parmi lesquels la possibilité de reconstruire des coupes à partir de données de projection incomplètes, de diminuer l’irradiation du patient en TDM et de mieux corriger les artefacts d’atténuation en TEP et tomoscintigraphie.
- L’algorithme MLEM opère itérativement en multipliant chaque valeur de pixel j de la coupe par la moyenne pondérée (par les coefficient ri,j) des rapports entre les projections i acquises et estimées qui concernent ce pixel j.
Référence
[1] Mariano-Goulart D. Reconstruction tomographique en imagerie médicale. EMC (Elsevier Masson SAS, Paris), Radiodiagnostic – Principes et techniques d’imagerie. 35-105-A-10 ; 2015.
 |
Chapitre suivant |
 |
Retour au sommaire |
